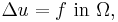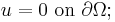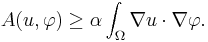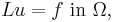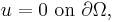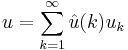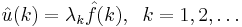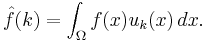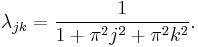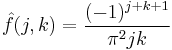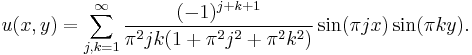Elliptic boundary value problem
In mathematics, an elliptic boundary value problem is a special kind of boundary value problem which can be thought of as the stable state of an evolution problem. For example, the Dirichlet problem for the Laplacian gives the eventual distribution of heat in a room several hours after the heating is turned on.
Differential equations describe a large class of natural phenomena, from the heat equation describing the evolution of heat in (for instance) a metal plate, to the Navier-Stokes equation describing the movement of fluids, including Einstein's equations describing the physical universe in a relativistic way. Although all these equations are boundary value problems, they are further subdivided into categories. This is necessary because each category must be analyzed using different techniques. The present article deals with the category of boundary value problems known as linear elliptic problems.
Boundary value problems and partial differential equations specify relations between two or more quantities. For instance, in the heat equation, the rate of change of temperature at a point is related to the difference of temperature between that point and the nearby points so that, over time, the heat flows from hotter points to cooler points. Boundary value problems can involve space, time and other quantities such as temperature, velocity, pressure, magnetic field, etc...
Some problems do not involve time. For instance, if one hangs a clothesline between the house and a tree, then in the absence of wind, the clothesline will not move and will adopt a gentle hanging curved shape known as the catenary [1]. This curved shape can be computed as the solution of a differential equation relating position, tension, angle and gravity, but since the shape does not change over time, there is no time variable.
Elliptic boundary value problems are a class of problems which do not involve the time variable, and instead only depend on space variables.
It is not possible to discuss elliptic boundary value problems in more detail without referring to calculus in multiple variables.
Unless otherwise noted, all facts presented in this article can be found in [2].
Contents |
The main example
In two dimensions, let 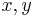 be the coordinates. We will use the notation
be the coordinates. We will use the notation 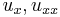 for the first and second partial derivatives of
for the first and second partial derivatives of  with respect to
with respect to  , and a similar notation for
, and a similar notation for  . We will use the symbols
. We will use the symbols 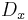 and
and 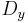 for the partial differential operators in
for the partial differential operators in  and
and  . The second partial derivatives will be denoted
. The second partial derivatives will be denoted 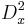 and
and 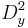 . We also define the gradient
. We also define the gradient 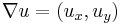 , the Laplace operator
, the Laplace operator 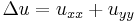 and the divergence
and the divergence 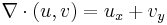 . Note from the definitions that
. Note from the definitions that  .
.
The main example for boundary value problems is the Laplace operator,
where  is a region in the plane and
is a region in the plane and 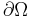 is the boundary of that region. The function
is the boundary of that region. The function  is known data and the solution
is known data and the solution  is what must be computed. This example has the same essential properties as all other elliptic boundary value problems.
is what must be computed. This example has the same essential properties as all other elliptic boundary value problems.
The solution  can be interpreted as the stationary or limit distribution of heat in a metal plate shaped like
can be interpreted as the stationary or limit distribution of heat in a metal plate shaped like  , if this metal plate has its boundary adjacent to ice (which is kept at zero degrees, thus the Dirichlet boundary condition.) The function
, if this metal plate has its boundary adjacent to ice (which is kept at zero degrees, thus the Dirichlet boundary condition.) The function  represents the intensity of heat generation at each point in the plate (perhaps there is an electric heater resting on the metal plate, pumping heat into the plate at rate
represents the intensity of heat generation at each point in the plate (perhaps there is an electric heater resting on the metal plate, pumping heat into the plate at rate  , which does not vary over time, but may be nonuniform in space on the metal plate.) After waiting for a long time, the temperature distribution in the metal plate will approach
, which does not vary over time, but may be nonuniform in space on the metal plate.) After waiting for a long time, the temperature distribution in the metal plate will approach  .
.
Nomenclature
Let 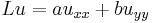 where
where  and
and  are constants.
are constants. 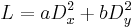 is called a second order differential operator. If we formally replace the derivatives
is called a second order differential operator. If we formally replace the derivatives 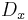 by
by  and
and 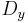 by
by  , we obtain the expression
, we obtain the expression
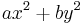 .
.
If we set this expression equal to some constant  , then we obtain either an ellipse (if
, then we obtain either an ellipse (if 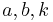 are all the same sign) or a hyperbola (if
are all the same sign) or a hyperbola (if  and
and  are of opposite signs.) For that reason,
are of opposite signs.) For that reason,  is said to be elliptic when
is said to be elliptic when 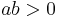 and hyperbolic if
and hyperbolic if 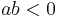 . Similarly, the operator
. Similarly, the operator 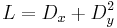 leads to a parabola, and so this
leads to a parabola, and so this  is said to be parabolic.
is said to be parabolic.
We now generalize the notion of ellipticity. While it may not be obvious that our generalization is the right one, it turns out that it does preserve most of the necessary properties for the purpose of analysis.
General linear elliptic boundary value problems of the second degree
Let  be the space variables. Let
be the space variables. Let 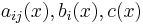 be real valued functions of
be real valued functions of 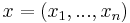 . Let
. Let  be a second degree linear operator. That is,
be a second degree linear operator. That is,
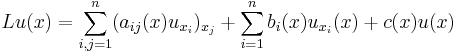 (divergence form).
(divergence form).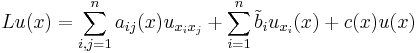 (nondivergence form)
(nondivergence form)
We have used the subscript 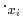 to denote the partial derivative with respect to the space variable
to denote the partial derivative with respect to the space variable  . The two formulae are equivalent, provided that
. The two formulae are equivalent, provided that
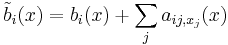 .
.
In matrix notation, we can let 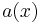 be an
be an 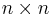 matrix valued function of
matrix valued function of  and
and 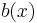 be a
be a  -dimensional column vector-valued function of
-dimensional column vector-valued function of  , and then we may write
, and then we may write
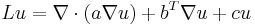 (divergence form).
(divergence form).
One may assume, without loss of generality, that the matrix  is symmetric (that is, for all
is symmetric (that is, for all 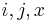 ,
, 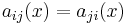 . We make that assumption in the rest of this article.
. We make that assumption in the rest of this article.
We say that the operator  is elliptic if, for some constant
is elliptic if, for some constant 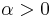 , any of the following equivalent conditions hold:
, any of the following equivalent conditions hold:
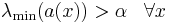 (see eigenvalue).
(see eigenvalue).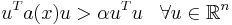 .
.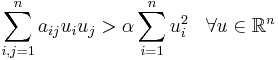 .
.
An elliptic boundary value problem is then a system of equations like
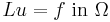 (the PDE) and
(the PDE) and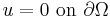 (the boundary value).
(the boundary value).
This particular example is the Dirichlet problem. The Neumann problem is
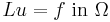 and
and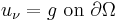
where 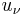 is the derivative of
is the derivative of  in the direction of the outwards pointing normal of
in the direction of the outwards pointing normal of 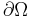 . In general, if
. In general, if  is any trace operator, one can construct the boundary value problem
is any trace operator, one can construct the boundary value problem
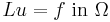 and
and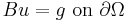 .
.
In the rest of this article, we assume that  is elliptic and that the boundary condition is the Dirichlet condition
is elliptic and that the boundary condition is the Dirichlet condition 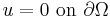 .
.
Sobolev spaces
The analysis of elliptic boundary value problems requires some fairly sophisticated tools of functional analysis. We require the space 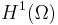 , the Sobolev space of "once-differentiable" functions on
, the Sobolev space of "once-differentiable" functions on  , such that both the function
, such that both the function  and its partial derivatives
and its partial derivatives 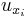 ,
, 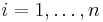 are all square integrable. There is a subtlety here in that the partial derivatives must be defined "in the weak sense" (see the article on Sobolev spaces for details.) The space
are all square integrable. There is a subtlety here in that the partial derivatives must be defined "in the weak sense" (see the article on Sobolev spaces for details.) The space 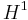 is a Hilbert space, which accounts for much of the ease with which these problems are analyzed.
is a Hilbert space, which accounts for much of the ease with which these problems are analyzed.
The discussion in details of Sobolev spaces is beyond the scope of this article, but we will quote required results as they arise.
Unless otherwise noted, all derivatives in this article are to be interpreted in the weak, Sobolev sense. We use the term "strong derivative" to refer to the classical derivative of calculus. We also specify that the spaces 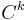 ,
, 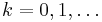 consist of functions that are
consist of functions that are  times strongly differentiable, and that the
times strongly differentiable, and that the  th derivative is continuous.
th derivative is continuous.
Weak or variational formulation
The first step to cast the boundary value problem as in the language of Sobolev spaces is to rephrase it in its weak form. Consider the Laplace problem 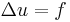 . Multiply each side of the equation by a "test function"
. Multiply each side of the equation by a "test function"  and integrate by parts using Green's theorem to obtain
and integrate by parts using Green's theorem to obtain
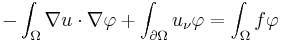 .
.
We will be solving the Dirichlet problem, so that 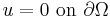 . For technical reasons, it is useful to assume that
. For technical reasons, it is useful to assume that  is taken from the same space of functions as
is taken from the same space of functions as  is so we also assume that
is so we also assume that 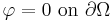 . This gets rid of the
. This gets rid of the 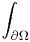 term, yielding
term, yielding
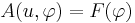 (*)
(*)
where
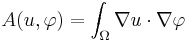 and
and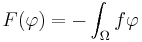 .
.
If  is a general elliptic operator, the same reasoning leads to the bilinear form
is a general elliptic operator, the same reasoning leads to the bilinear form
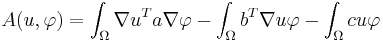 .
.
We do not discuss the Neumann problem but note that it is analyzed in a similar way.
Continuous and coercive bilinear forms
The map 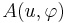 is defined on the Sobolev space
is defined on the Sobolev space 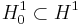 of functions which are once differentiable and zero on the boundary
of functions which are once differentiable and zero on the boundary 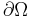 , provided we impose some conditions on
, provided we impose some conditions on 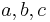 and
and  . There are many possible choices, but for the purpose of this article, we will assume that
. There are many possible choices, but for the purpose of this article, we will assume that
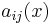 is continuously differentiable on
is continuously differentiable on  for
for 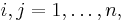
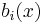 is continuous on
is continuous on 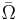 for
for 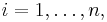
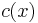 is continuous on
is continuous on 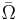 and
and is bounded.
is bounded.
The reader may verify that the map 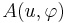 is furthermore bilinear and continuous, and that the map
is furthermore bilinear and continuous, and that the map 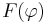 is linear in
is linear in  , and continuous if (for instance)
, and continuous if (for instance)  is square integrable.
is square integrable.
We say that the map  is coercive if there is an
is coercive if there is an 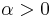 for all
for all 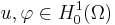 ,
,
This is trivially true for the Laplacian (with 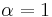 ) and is also true for an elliptic operator if we assume
) and is also true for an elliptic operator if we assume 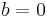 and
and 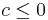 . (Recall that
. (Recall that 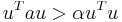 when
when  is elliptic.)
is elliptic.)
Existence and uniqueness of the weak solution
One may show, via the Lax–Milgram lemma, that whenever 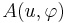 is coercive and
is coercive and 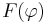 is continuous, then there exists a unique solution
is continuous, then there exists a unique solution 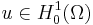 to the weak problem (*).
to the weak problem (*).
If further 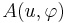 is symmetric (i.e.,
is symmetric (i.e., 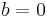 ), one can show the same result using the Riesz representation theorem instead.
), one can show the same result using the Riesz representation theorem instead.
This relies on the fact that 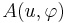 forms an inner product on
forms an inner product on 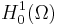 , which itself depends on Poincaré's inequality.
, which itself depends on Poincaré's inequality.
Strong solutions
We have shown that there is a 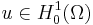 which solves the weak system, but we do not know if this
which solves the weak system, but we do not know if this  solves the strong system
solves the strong system
Even more vexing is that we are not even sure that  is twice differentiable, rendering the expressions
is twice differentiable, rendering the expressions 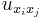 in
in 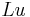 apparently meaningless. There are many ways to remedy the situation, the main one being regularity.
apparently meaningless. There are many ways to remedy the situation, the main one being regularity.
Regularity
A regularity theorem for a linear elliptic boundary value problem of the second order takes the form
Theorem If (some condition), then the solution  is in
is in 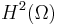 , the space of "twice differentiable" functions whose second derivatives are square integrable.
, the space of "twice differentiable" functions whose second derivatives are square integrable.
There is no known simple condition necessary and sufficient for the conclusion of the theorem to hold, but the following conditions are known to be sufficient:
- The boundary of
 is
is 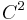 , or
, or  is convex.
is convex.
It may be tempting to infer that if 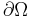 is piecewise
is piecewise 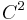 then
then  is indeed in
is indeed in 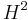 , but that is unfortunately false.
, but that is unfortunately false.
Almost everywhere solutions
In the case that 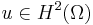 then the second derivatives of
then the second derivatives of  are defined almost everywhere, and in that case
are defined almost everywhere, and in that case 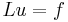 almost everywhere.
almost everywhere.
Strong solutions
One may further prove that if the boundary of 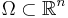 is a smooth manifold and
is a smooth manifold and  is infinitely differentiable in the strong sense, then
is infinitely differentiable in the strong sense, then  is also infinitely differentiable in the strong sense. In this case,
is also infinitely differentiable in the strong sense. In this case, 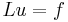 with the strong definition of the derivative.
with the strong definition of the derivative.
The proof of this relies upon an improved regularity theorem that says that if 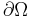 is
is 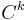 and
and 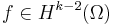 ,
, 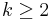 , then
, then 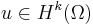 , together with a Sobolev imbedding theorem saying that functions in
, together with a Sobolev imbedding theorem saying that functions in 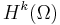 are also in
are also in 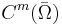 whenever
whenever 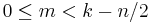 .
.
Numerical solutions
While in exceptional circumstances, it is possible to solve elliptic problems explicitly, in general it is an impossible task. The natural solution is to approximate the elliptic problem with a simpler one and to solve this simpler problem on a computer.
Because of the good properties we have enumerated (as well as many we have not), there are extremely efficient numerical solvers for linear elliptic boundary value problems (see finite element method, finite difference method and spectral method for examples.)
Eigenvalues and eigensolutions
Another Sobolev imbedding theorem states that the inclusion 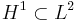 is a compact linear map. Equipped with the spectral theorem for compact linear operators, one obtains the following result.
is a compact linear map. Equipped with the spectral theorem for compact linear operators, one obtains the following result.
Theorem Assume that 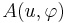 is coercive, continuous and symmetric. The map
is coercive, continuous and symmetric. The map 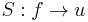 from
from 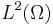 to
to 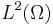 is a compact linear map. It has a basis of eigenvectors
is a compact linear map. It has a basis of eigenvectors 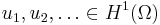 and matching eigenvalues
and matching eigenvalues 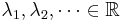 such that
such that
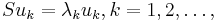
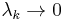 as
as 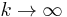 ,
,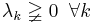 ,
,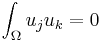 whenever
whenever 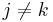 and
and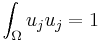 for all
for all 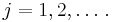
Series solutions and the importance of eigensolutions
If one has computed the eigenvalues and eigenvectors, then one may find the "explicit" solution of 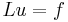 ,
,
via the formula
where
(See Fourier series.)
The series converges in 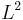 . Implemented on a computer using numerical approximations, this is known as the spectral method.
. Implemented on a computer using numerical approximations, this is known as the spectral method.
An example
Consider the problem
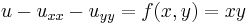 on
on 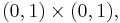
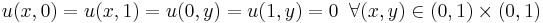 (Dirichlet conditions).
(Dirichlet conditions).
The reader may verify that the eigenvectors are exactly
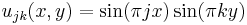 ,
, 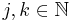
with eigenvalues
The Fourier coefficients of 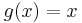 can be looked up in a table, getting
can be looked up in a table, getting 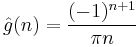 . Therefore,
. Therefore,
yielding the solution
Maximum principle
There are many variants of the maximum principle. We give a simple one.
Theorem. (Weak maximum principle.) Let 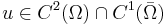 , and assume that
, and assume that 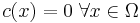 . Say that
. Say that 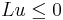 in
in  . Then
. Then 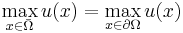 . In other words, the maximum is attained on the boundary.
. In other words, the maximum is attained on the boundary.
A strong maximum principle would conclude that 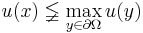 for all
for all 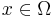 unless
unless  is constant.
is constant.